You are here: OxNotes Home › GCSE/IGCSE Notes › IGCSE Maths › Ratios
Ratios can always be treated like fractions
If there is a bag of blue and red counters in the ratio 4:5,
it means that for every 4 blue counters there are 5 red counters.
So if there were 16 blue counters, there would be 20 red counters.
This can be worked out by multiplying both sides by the same amount. In the above case, 4 has been multiplied by 4 to get 16. this means that to find the red counters we have to multiply 5 by 4. This will give us 20.
Ratios can also be written as a fraction, so there are 4/5 as many blue counters as red counters. if there are 30 red counters, then the blue counters can be worked out by:
30 * 4/5 = 24
Ratios can always be treated like fractions
If there is a bag of blue and red counters in the ratio 4:5,
it means that for every 4 blue counters there are 5 red counters.
So if there were 16 blue counters, there would be 20 red counters.
This can be worked out by multiplying both sides by the same amount. In the above case, 4 has been multiplied by 4 to get 16. this means that to find the red counters we have to multiply 5 by 4. This will give us 20.
Ratios can also be written as a fraction, so there are 4/5 as many blue counters as red counters. if there are 30 red counters, then the blue counters can be worked out by:
30 * 4/5 = 24
Simplifying Ratios
Ratios are reduced just like fractions are. Both sides are divided by the same amount to find the simplest form:
15:18 ÷3 = 5:6
5:6 is the simplest form, as it can't be divided further.
The ratio can also be reduced to a 1:n form. This is usually the most helpful as it allows the ratio to be seen clearly. To reduce a fraction to this form, divide both sides by the smallest side.
E.g. 3:27 ---> 1:9
15:18 ÷3 = 5:6
5:6 is the simplest form, as it can't be divided further.
The ratio can also be reduced to a 1:n form. This is usually the most helpful as it allows the ratio to be seen clearly. To reduce a fraction to this form, divide both sides by the smallest side.
E.g. 3:27 ---> 1:9
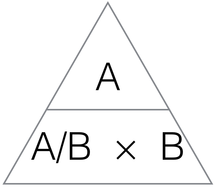
The ratio formula triangle:
This formula triangle can be used in questions such as:
"A necklace is made using blue and red beads in the ratio 7:2, if 30 blue beads are used, how many red beads are used?"
"A necklace is made using blue and red beads in the ratio 7:2, if 30 blue beads are used, how many red beads are used?"
The ratio must always be the right way around, the first number in the ratio always going on the top (A:B).
The above question can be worked out:
A = Number of blue beads
B = Number of red beads
A/B = 3.5 (7/2)
The part of the triangle that is covered up is the value that we need, which in this case would be 'B'. With the B covered up we are left with 'A' divided by 'A/B'. this would be 30 ÷ 3.5 = 8.57 (2dp)
The above question can be worked out:
A = Number of blue beads
B = Number of red beads
A/B = 3.5 (7/2)
The part of the triangle that is covered up is the value that we need, which in this case would be 'B'. With the B covered up we are left with 'A' divided by 'A/B'. this would be 30 ÷ 3.5 = 8.57 (2dp)
Proportional ratios/division
In these types of questions, an amount is split into a certain ratio.
For example:
"£21,000 is to be split between Emma and Jake in the ratio 4:3. find the two amounts that they each get"
To do this type of question:
For example:
"£21,000 is to be split between Emma and Jake in the ratio 4:3. find the two amounts that they each get"
To do this type of question:
- The two sides of the ratio have to be added up first (4+3=7). This will give you the total parts that the £21,000 have to be split into.
- Find how much one part is worth. To do this, divide the total amount by the amount of parts (£21,000 ÷ 7 = £3,000)
- Find out how much each person gets: Emma: 4 parts: £3,000 x 4 = £12,000 Jake: 3 parts: £3,000 x 3 = £9,000
Where next? More IGCSE Maths notes
- Go to IGCSE Maths (all Maths notes)
- StudentSpace Blog
- Search by keyword: